AVL Tree

AVL Tree

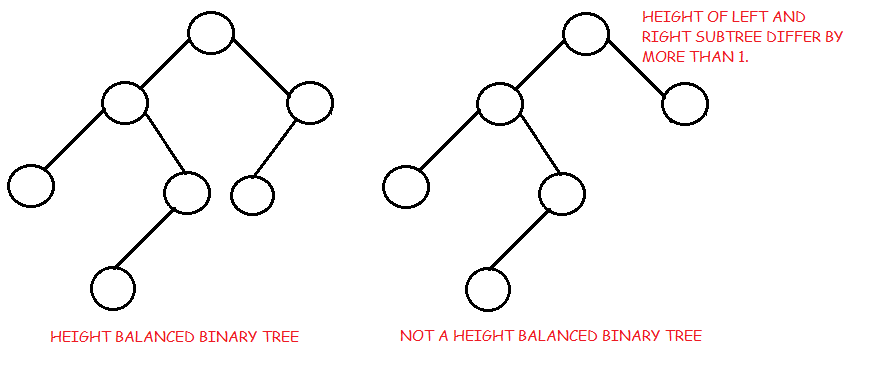
AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes.

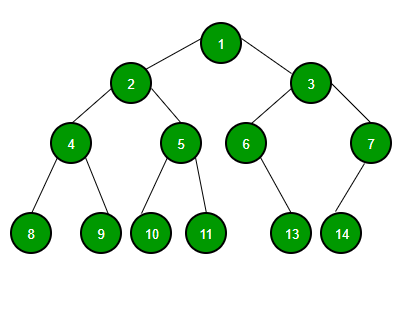
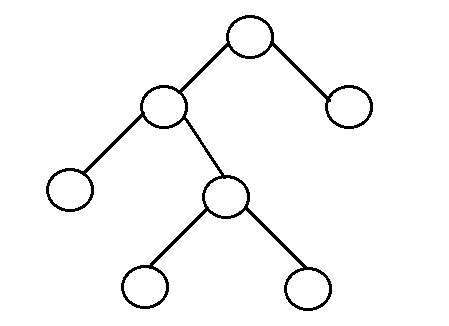
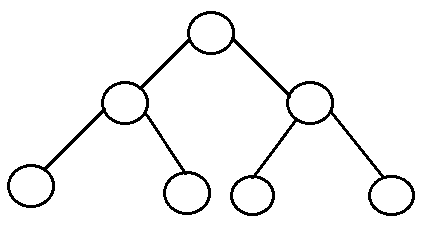
Example of Tree that is an AVL Tree

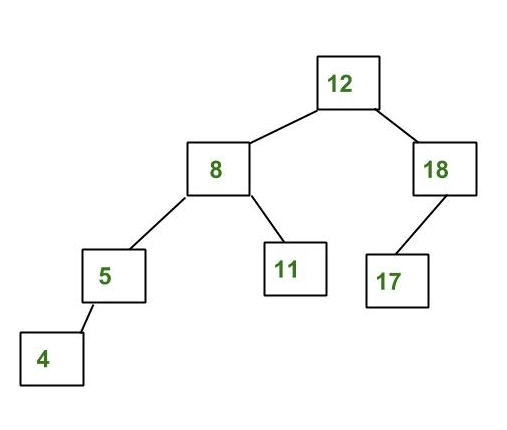
The tree above is AVL because the difference between heights of left and right subtrees for every node is less than or equal to 1.

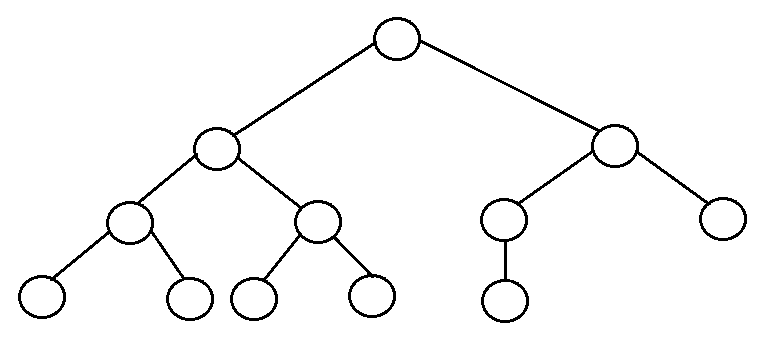
Example Tree that is not an AVL Tree

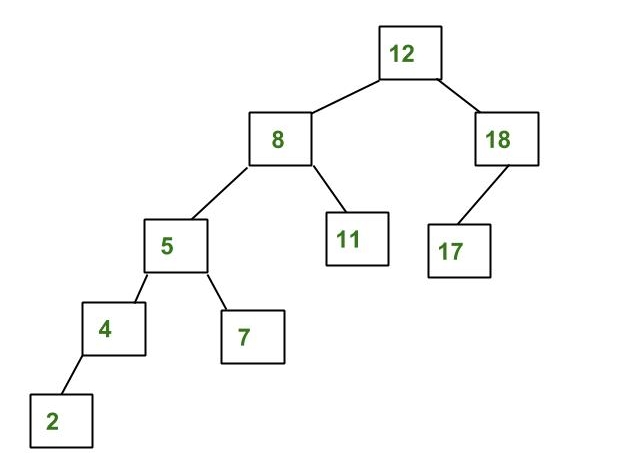
The tree above is not AVL because the differences between heights of left and right subtrees for 8 and 18 is greater than 1.

Most of the BST operations for example search, max, min, insert, delete, etc. take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary Tree. If we make sure that height of the tree remains O(Log n) after every insertion and deletion, then we can guarantee an upper bound of  O(Log n) for all these operations. The height of an AVL tree is always O(Log n) where n is the number of nodes in the tree.

Source:

- https://www.geeksforgeeks.org/avl-tree-set-1-insertion/

Data Structure Summary

Circular Singly Linked List :

In a Circular Singly Linked List, the last node of the list contains a pointer to the first note of the list. We can have a circular singly linked list as well as a double linked list.

We traverse a circular singly linked list until we reach the same node where we started. The circular singly linked list has no beginning and no ending. There is no null value present in the next part of any of the nodes.

 Circular Linked List is mostly used in task maintenance in operating systems. There are many examples where circular linked list is being used in computer science including browser surfing where a record of pages visited in the past by the user, is maintained in the form of circular linked lists and can be accessed again in clicking the previous button.

Doubly Linked List :

A Doubly Linked List ( DLL ) contains an extra pointer, typically called previous pointer, together with next pointer and data which are there in singly linked list.

Double linked list advantages over singly linked list :

1. A DLL can be traversed in both forward and backward direction.
2. The delete operation in DLL is more efficient if pointer to the node to be deleted is given.
3. We can quickly inner a new node before a given node. In singly linked list, to delete a node, pointer to the previous node is needed. To get this pervious node, sometimes the list is traversed. In DLL, we can get the previous node using previous pointer.

Disadvantages over singly linked list :

1. Every node of DLL Require extra space for an previous pointer. It is possible to implement DLL with single pointer though.
2. All operations require an extra pointer previous to be maintained. For example, in insertion, we need to modify previous pointers together with next pointers. For example in following functions for insertions at different positions, we need 1 or 2 extra steps to set previous pointer.

Circular Doubly Linked List :

Circular doubly linked list is a more complexed type of data structure in which a node contain pointers to its previous node as well as the next code. Circular doubly linked list doesn't contain NULL in any of the node. The last node of the list contain the address of the first node of the list. The first ndoe of the list also contain address of the last node in its previous pointer.

Due to the fact that a circular doubly linked list contains three parts in its structure therefore, it demands more space per node and more expensive basic operations. However, a circular doubly linked list provides easy manipulation of the pointers and the searching becomes twice as efficient.

Hash Table

Hash Table organizes data so you can quickly look up values for a given key.

Strengths:

• Fast lookups. lookups take O(1) time on average.
• Flexible keys. Most data types can be used for keys, as long as they're washable.

Weaknesses:

• Slow worst-case lookups. Lookups take O(n) time in the worst case.
• Unordered. Keys aren't stored in a special order. If you're looking for the smallest key, the largest key, or all the keys in a range, you'll need to look through every key to find it.
• Single-directional lookups. While you can look up the value for a given key in O(1) time, looking up the keys for a given value requires looping through the whole dataset -O(n) time.
• Not cache-friendly. Many hash table implementations use linked lists which don't put data next to each other in memory.

Hashing

A hash function is a mathematical function which takes an input and produces an output. i.e. Y=H(X) , where X is the input, H() is the hash functionand Y is the output.

• Hash function are one-way:

Given an input, the hash function can generate a "hashed" output very quickly.

• Hash for a given input is always the same:

For the given input, the hash function will always produce the same output. However, If the input in altered even slightly, the "hashed" output is completely different.

Binary Tree Data Structure

A tree whose elements have at most 2 children is called a binary tree. since each element in a binary can have only 2 children, we typically name them the left and right child.

A Binary Tree node contains following parts:

• Data
• Pointer to left child
• Pointer to right child

Types of Binary Tree 

• Rooted Binary Tree: it has a root node and every node has almost to children.

• Perfect Binary Tree: it is a binary tree in which all interior nodes have two children and all leaves have the same depth or same level.

• Complete Binary Tree : Binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

• Balanced Binary Tree: Bnary Tree is height balanced if it satisfies the following constraints:

1. The left and right subtrees height differ by at most one, AND
2. The left sub tree is balanced, AND
3. The right subtree is balanced

An empty tree is height is balanced.

• Degenerate Tree:  its a tree is where each parent node has only one child node. it behave like linked list.

Source :

• https://www.javatpoint.com/circular-singly-linked-list
• https://www.geeksforgeeks.org/doubly-linked-list/
• https://www.javatpoint.com/circular-doubly-linked-list
• https://www.studytonight.com/data-structures/introduction-to-binary-trees
  https://www.geeksforgeeks.org/binary-tree-data-structure/#summation
  https://www.interviewcake.com/concept/java/hash-map
  https://hackernoon.com/blockchain-demystified-under-the-hood-of-blockchain-fd4f3426bb20