Final Review
Nama : Joshua Rafael
NIM : 2301902182
Kelas : CB01 - CL
Dosen : - Ferdinand Ariandy Luwinda (D4522)
- Henry Chong (D4460)
Linked List
Circular Singly Linked List :
In a Circular Singly Linked List, the last node of the list contains a pointer to the first note of the list. We can have a circular singly linked list as well as a double linked list.
We traverse a circular singly linked list until we reach the same node where we started. The circular singly linked list has no beginning and no ending. There is no null value present in the next part of any of the nodes.
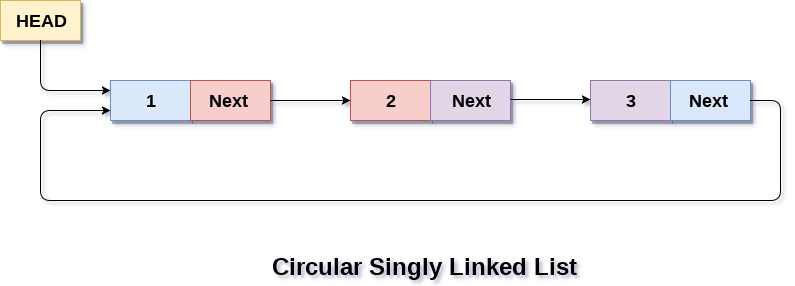
Circular Linked List is mostly used in task maintenance in operating systems. There are many examples where circular linked list is being used in computer science including browser surfing where a record of pages visited in the past by the user, is maintained in the form of circular linked lists and can be accessed again in clicking the previous button.
Doubly Linked List :
A Doubly Linked List ( DLL ) contains an extra pointer, typically called previous pointer, together with next pointer and data which are there in singly linked list.
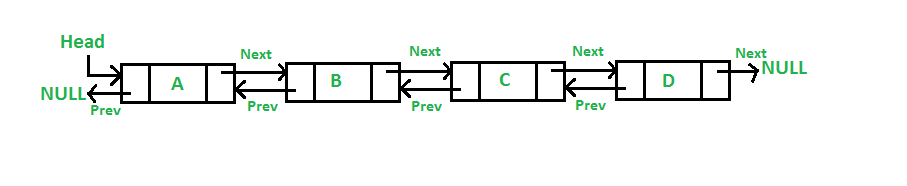
Double linked list advantages over singly linked list :
- A DLL can be traversed in both forward and backward direction.
- The delete operation in DLL is more efficient if pointer to the node to be deleted is given.
- We can quickly inner a new node before a given node. In singly linked list, to delete a node, pointer to the previous node is needed. To get this pervious node, sometimes the list is traversed. In DLL, we can get the previous node using previous pointer.
Disadvantages over singly linked list :
- Every node of DLL Require extra space for an previous pointer. It is possible to implement DLL with single pointer though.
- All operations require an extra pointer previous to be maintained. For example, in insertion, we need to modify previous pointers together with next pointers. For example in following functions for insertions at different positions, we need 1 or 2 extra steps to set previous pointer.
Insertion :
A node can be added in four ways :
- At the front of the DLL
- After a given node
- At the end of the DLL
- Before a given node.
Deletion :
There are 4 conditions we should pay attention when deleting :
- The node to be deleted is the only node in linked list.
- The node to be deleted is head
- The node to be deleted is tail.
- The node to be deleted is not head or tail.
Circular Doubly Linked List :
Circular doubly linked list is a more complexed type of data structure in which a node contain pointers to its previous node as well as the next code. Circular doubly linked list doesn't contain NULL in any of the node. The last node of the list contain the address of the first node of the list. The first ndoe of the list also contain address of the last node in its previous pointer.
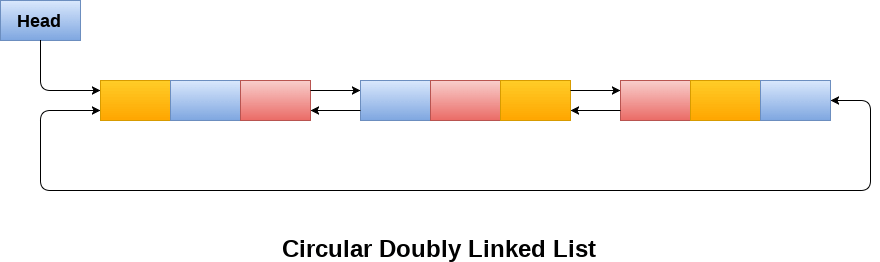
Due to the fact that a circular doubly linked list contains three parts in its structure therefore, it demands more space per node and more expensive basic operations. However, a circular doubly linked list provides easy manipulation of the pointers and the searching becomes twice as efficient.
Source :
- https://www.javatpoint.com/circular-singly-linked-list
- https://www.geeksforgeeks.org/doubly-linked-list/
- https://www.javatpoint.com/circular-doubly-linked-list
Hash Table

Hash Table organizes data so you can quickly look up values for a given key.
Strengths:
- Fast lookups. lookups take O(1) time on average.
- Flexible keys. Most data types can be used for keys, as long as they're washable.
Weaknesses:
- Slow worst-case lookups. Lookups take O(n) time in the worst case.
- Unordered. Keys aren't stored in a special order. If you're looking for the smallest key, the largest key, or all the keys in a range, you'll need to look through every key to find it.
- Single-directional lookups. While you can look up the value for a given key in O(1) time, looking up the keys for a given value requires looping through the whole dataset -O(n) time.
- Not cache-friendly. Many hash table implementations use linked lists which don't put data next to each other in memory.
| Average | Worst Case | |
|---|---|---|
| space | ||
| insert | ||
| lookup | ||
| delete |
Hash Maps are built on arrays
Arrays are pretty similar to hash maps already. Array let you quickly look up the vcalue for a given "key". except the keys are called "indices" and we dont get to pick them they're always sequential integers (0,1,2,3,etc). Think of a hash map as a hack on top of an array to let us use flexible keys instead of being stuck with sequential integers "indices".
All we need is a function to convert a key into an array index(an integer). That function is called a hashing function.

To look up the value for a given key, we just run the key through our hashing function to get the index to go to in our underlying array to grab the value.

The result is 429. But if we only have 30 slots in our array we'll use the modulus operator (%). Modding our sum by 30 ensures we get a whole number that's less than 30 (and at least 0) :
429 % 30 = 9
The building Blocks of BlockChain
Hashing
A hash function is a mathematical function which takes an input and produces an output. i.e. Y=H(X) , where X is the input, H() is the hash functionand Y is the output.
- Hash function are one-way:
Given an input, the hash function can generate a "hashed" output very quickly.

- Hash for a given input is always the same:
For the given input, the hash function will always produce the same output. However, If the input in altered even slightly, the "hashed" output is completely different.


- The Hash output is always a fixed length:
The output is always a fixed length, irrespective of the size of the input string.

BlockChain technology employs Hashing Algorithms as the building blocks to create secure blocks of data.
Given a hashed output with some criteria, can you determine what input will generate that output? i.e. what input string, when passed through a hashing function(eg. SHA 256),will generate an output string that ends in .....abc276.
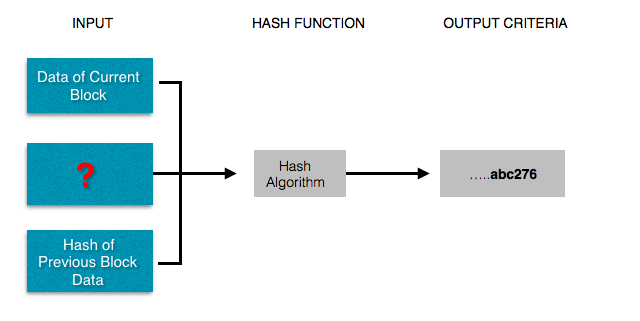
Given the nature of hashing algorithms, weknow that to answer this question is difficult and ill possibly require a brute force approach. After trying several million different combination of inputs, finally one input string may generate an output string like ed892349837abd2349abc276,
which will finally match the criteria.
Binary Tree Data Structure
A tree whose elements have at most 2 children is called a binary tree. since each element in a binary can have only 2 children, we typically name them the left and right child.
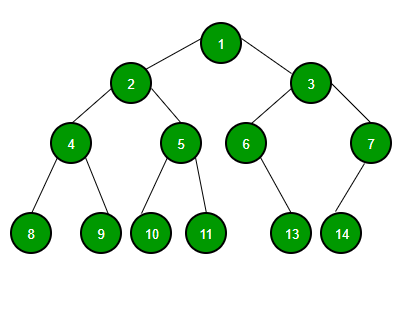
A Binary Tree node contains following parts:
- Data
- Pointer to left child
- Pointer to right child
Types of Binary Tree
- Rooted Binary Tree: it has a root node and every node has almost to children.
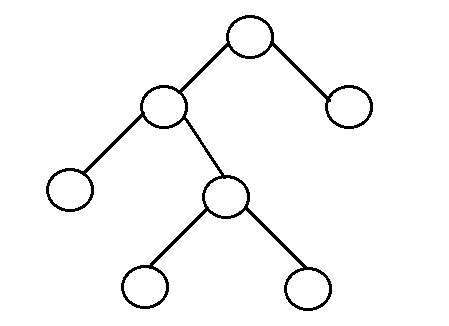
- Perfect Binary Tree: it is a binary tree in which all interior nodes have two children and all leaves have the same depth or same level.
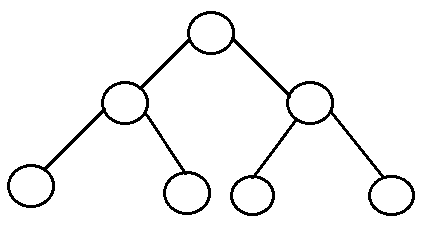
- Complete Binary Tree : Binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
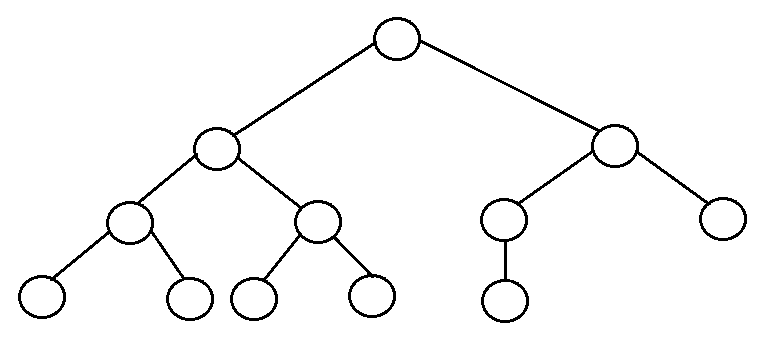
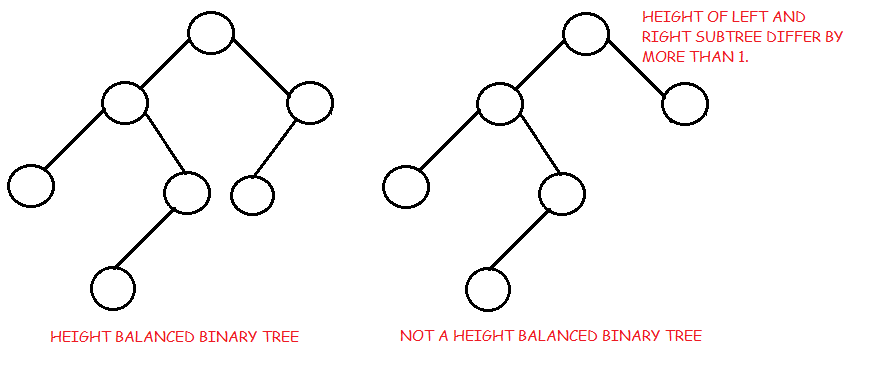
- Balanced Binary Tree: Bnary Tree is height balanced if it satisfies the following constraints:
- The left and right subtrees height differ by at most one, AND
- The left sub tree is balanced, AND
- The right subtree is balanced
An empty tree is height is balanced.
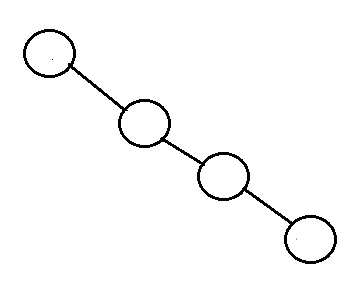
- Degenerate Tree: its a tree is where each parent node has only one child node. it behave like linked list.
Source:
Data Structure Summary
Circular Singly Linked List :
In a Circular Singly Linked List, the last node of the list contains a pointer to the first note of the list. We can have a circular singly linked list as well as a double linked list.
We traverse a circular singly linked list until we reach the same node where we started. The circular singly linked list has no beginning and no ending. There is no null value present in the next part of any of the nodes.

Circular Linked List is mostly used in task maintenance in operating systems. There are many examples where circular linked list is being used in computer science including browser surfing where a record of pages visited in the past by the user, is maintained in the form of circular linked lists and can be accessed again in clicking the previous button.
Doubly Linked List :
A Doubly Linked List ( DLL ) contains an extra pointer, typically called previous pointer, together with next pointer and data which are there in singly linked list.

Double linked list advantages over singly linked list :
- A DLL can be traversed in both forward and backward direction.
- The delete operation in DLL is more efficient if pointer to the node to be deleted is given.
- We can quickly inner a new node before a given node. In singly linked list, to delete a node, pointer to the previous node is needed. To get this pervious node, sometimes the list is traversed. In DLL, we can get the previous node using previous pointer.
Disadvantages over singly linked list :
- Every node of DLL Require extra space for an previous pointer. It is possible to implement DLL with single pointer though.
- All operations require an extra pointer previous to be maintained. For example, in insertion, we need to modify previous pointers together with next pointers. For example in following functions for insertions at different positions, we need 1 or 2 extra steps to set previous pointer.
Circular Doubly Linked List :
Circular doubly linked list is a more complexed type of data structure in which a node contain pointers to its previous node as well as the next code. Circular doubly linked list doesn't contain NULL in any of the node. The last node of the list contain the address of the first node of the list. The first ndoe of the list also contain address of the last node in its previous pointer.

Due to the fact that a circular doubly linked list contains three parts in its structure therefore, it demands more space per node and more expensive basic operations. However, a circular doubly linked list provides easy manipulation of the pointers and the searching becomes twice as efficient.










Hash Table

Hash Table organizes data so you can quickly look up values for a given key.
Strengths:
- Fast lookups. lookups take O(1) time on average.
- Flexible keys. Most data types can be used for keys, as long as they're washable.
Weaknesses:
- Slow worst-case lookups. Lookups take O(n) time in the worst case.
- Unordered. Keys aren't stored in a special order. If you're looking for the smallest key, the largest key, or all the keys in a range, you'll need to look through every key to find it.
- Single-directional lookups. While you can look up the value for a given key in O(1) time, looking up the keys for a given value requires looping through the whole dataset -O(n) time.
- Not cache-friendly. Many hash table implementations use linked lists which don't put data next to each other in memory.
Hashing
A hash function is a mathematical function which takes an input and produces an output. i.e. Y=H(X) , where X is the input, H() is the hash functionand Y is the output.
- Hash function are one-way:
Given an input, the hash function can generate a "hashed" output very quickly.

- Hash for a given input is always the same:
For the given input, the hash function will always produce the same output. However, If the input in altered even slightly, the "hashed" output is completely different.


Binary Tree Data Structure
A tree whose elements have at most 2 children is called a binary tree. since each element in a binary can have only 2 children, we typically name them the left and right child.

A Binary Tree node contains following parts:
- Data
- Pointer to left child
- Pointer to right child
Types of Binary Tree
- Rooted Binary Tree: it has a root node and every node has almost to children.

- Perfect Binary Tree: it is a binary tree in which all interior nodes have two children and all leaves have the same depth or same level.

- Complete Binary Tree : Binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

- Balanced Binary Tree: Bnary Tree is height balanced if it satisfies the following constraints:
- The left and right subtrees height differ by at most one, AND
- The left sub tree is balanced, AND
- The right subtree is balanced
An empty tree is height is balanced.

- Degenerate Tree: its a tree is where each parent node has only one child node. it behave like linked list.

Source :
- https://www.javatpoint.com/circular-singly-linked-list
- https://www.geeksforgeeks.org/doubly-linked-list/
- https://www.javatpoint.com/circular-doubly-linked-list
-
AVL Tree
AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes.
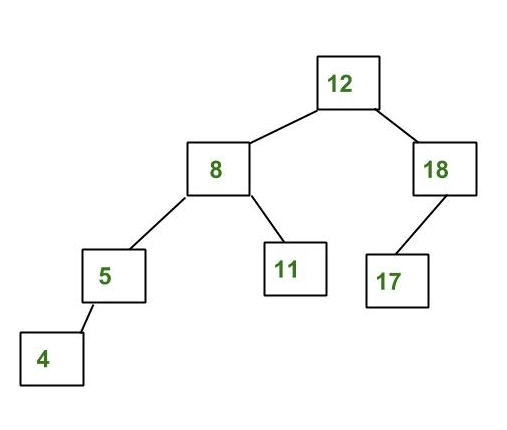
Example of Tree that is an AVL Tree

The tree above is AVL because the difference between heights of left and right subtrees for every node is less than or equal to 1.
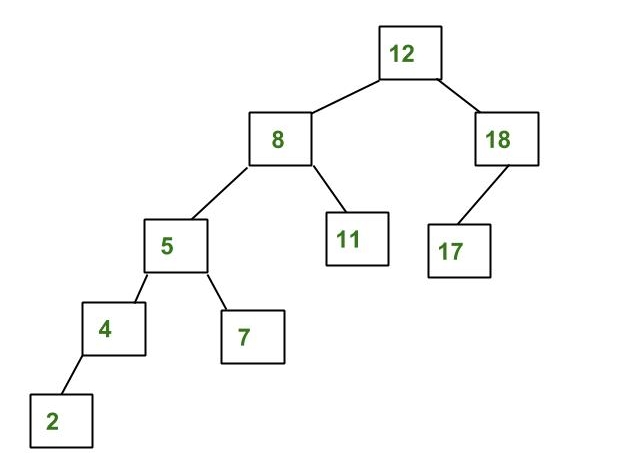
Example Tree that is not an AVL Tree

The tree above is not AVL because the differences between heights of left and right subtrees for 8 and 18 is greater than 1.
Most of the BST operations for example search, max, min, insert, delete, etc. take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary Tree. If we make sure that height of the tree remains O(Log n) after every insertion and deletion, then we can guarantee an upper bound of O(Log n) for all these operations. The height of an AVL tree is always O(Log n) where n is the number of nodes in the tree.
Source:
- https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
Heap & Tree
Heap Sort
Heap sort is a comparison based sorting technique based on Binary Heap data structure. It is similar to selection sort where we first find the maximum element and place the maximum element at the end. We repeat the same process for remaining element.
What is Binary Heap?
Let us first define a Complete Binary Tree. A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible
Let us first define a Complete Binary Tree. A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible
A Binary Heap is a Complete Binary Tree where items are stored in a special order such that value in a parent node is greater(or smaller) than the values in its two children nodes. The former is called as max heap and the latter is called min heap. The heap can be represented by binary tree or array.
Why array based representation for Binary Heap?
Since a Binary Heap is a Complete Binary Tree, it can be easily represented as array and array based representation is space efficient. If the parent node is stored at index I, the left child can be calculated by 2 * I + 1 and right child by 2 * I + 2 (assuming the indexing starts at 0).
Since a Binary Heap is a Complete Binary Tree, it can be easily represented as array and array based representation is space efficient. If the parent node is stored at index I, the left child can be calculated by 2 * I + 1 and right child by 2 * I + 2 (assuming the indexing starts at 0).
Heap Sort Algorithm for sorting in increasing order:
1. Build a max heap from the input data.
2. At this point, the largest item is stored at the root of the heap. Replace it with the last item of the heap followed by reducing the size of heap by 1. Finally, heapify the root of tree.
3. Repeat above steps while size of heap is greater than 1.
1. Build a max heap from the input data.
2. At this point, the largest item is stored at the root of the heap. Replace it with the last item of the heap followed by reducing the size of heap by 1. Finally, heapify the root of tree.
3. Repeat above steps while size of heap is greater than 1.
How to build the heap?
Heapify procedure can be applied to a node only if its children nodes are heapified. So the heapification must be performed in the bottom up order.
Heapify procedure can be applied to a node only if its children nodes are heapified. So the heapification must be performed in the bottom up order.
Tree Sort
Tree sort is a sorting algorithm that is based on Binary Search Tree data structure. It first creates a binary search tree from the elements of the input list or array and then performs an in-order traversal on the created binary search tree to get the elements in sorted order.
Source :